a/n: A friend @0xredJ has found this helpful and I decided to share my notes.
A time ago, Feynman noticed the ants in his kitchen would form trails to food sources. So, he enticed the ants with a sugar cube and disrupted them by drawing coloured trails on the ground. The ants didn’t care. Then he folded a paper bridge and waited for ants to step on them. Then he ferried the ants from one place to another. At the new location, the ants would initially be lost but over time form a nearly shortest path again.
This foreshadowed the development of Ant Colony Optimization and many more that describe the social behaviour of insects and in nature toward a target. Particle Swarm Optimization is a famous one, let’s see a video (plugging my code demo!).
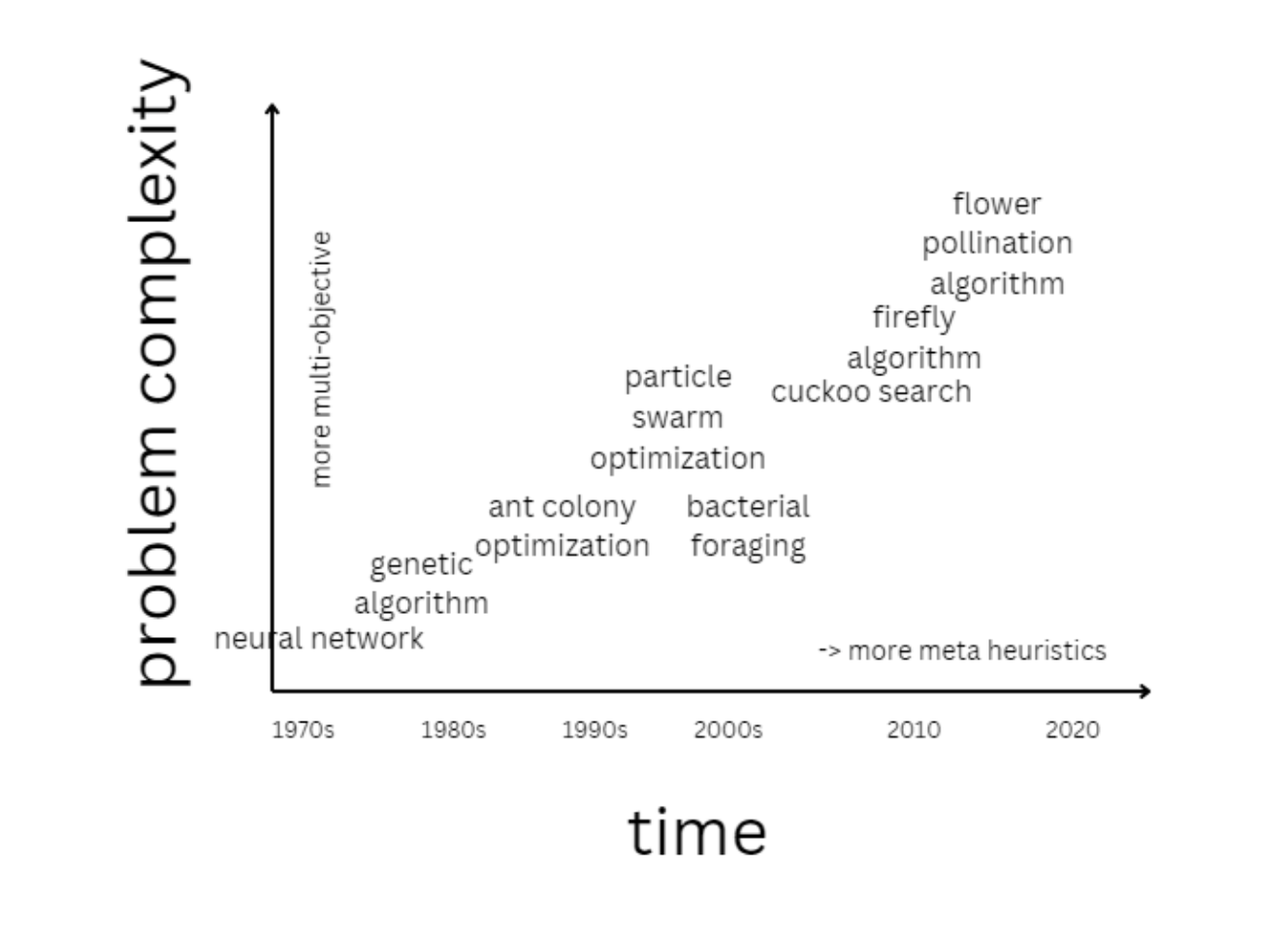
Of course, there are also bacteria, fireflies, cuckoos, flower polllination and living neurons which served as inspirations. You can see the development of these algorithms through time.
Flowcharts
What do these algorithms have in common?
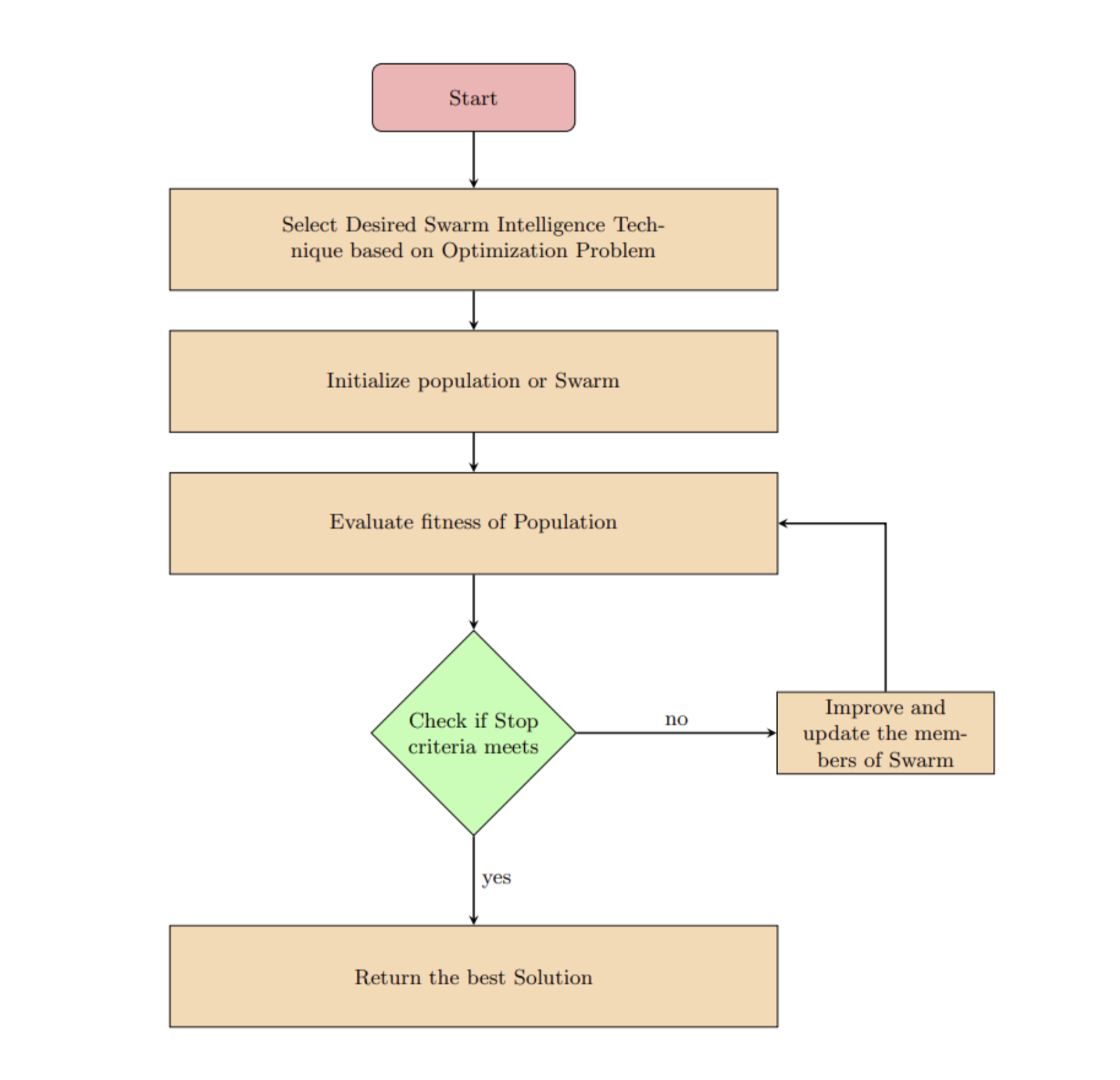
- Start. Initialize the population including the positions and velocities of particles. Define objective function $f(x, t)$ which could represent metrics like pollen density, or pest density within a particular sensing radius. The goal is to maximize $f(x^)$ where $x^$ is the global optimal solution.
- Evaluate objective function. For every particle, calculate personal best $f(x_i, t)$ at time $t$. Compare the current $f(x_i, t)$ with global best $f(x^*, best)$.
- Update. Changes in the velocity and position of individual members when there is a new best:
- New personal best. If $f(x_i, t) ≥ f(x_i, best)$: then $f(x_i, best) = f(x_i, t)$ and $p = x_i, t$
- New global best. If $f(x_i, t) ≥ f(x_i, best)$: then $f(x_i, best) = f(x_i, t)$ and $g = x_i, t$
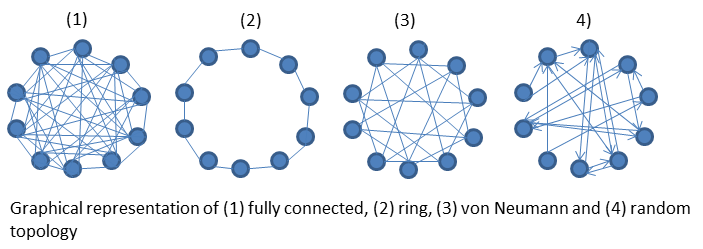
- Consider population topology. How many other nodes each node is connected to will affect the swarm algorithm efficiency. In some variants, individuals only directly share information with their dearest neighbours, forming a ‘local best’.
We compare this with conventional optimization algorithms:
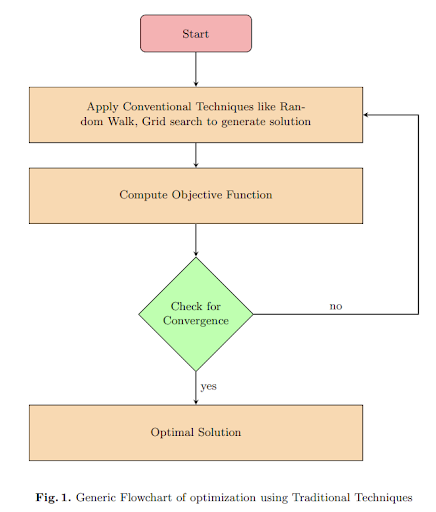
Key differences
Conventional optimization usually use deterministic rules to iteratively improve it’s solutions. The search process is guided by mathematical properties of the objecive function. Risk of local optima and coverge faster, guaranteed under specific conditions like smoothness and convexity.
Swarm intelligence uses a population of agents, with stochastic components. It’s better at escaping local optima, can perform better at non-continuous, non-differentiable and noisy problems. Likewise, also better at NP problems. NP problems like travelling salesman or knapsack problem involve finding the best solution in a very large number of possible combinations so parallelization helps. However, swarm intelligence is more exploratory and may take a longer time to converge.
Particle swarm optimization
Update rules - just take it and implement it in your own code:
Velocity updates: $v_i^{t+1} = v_i^t +r_1 \cdot c_1 \cdot(g-x_i^t)+r_2 \cdot c_2 \cdot(p-x_i^t)$
Position updates: $x_i^{t+1} = x_i^t + v_i^{t+1}$
$v_i^t$: the velocity of particle $i$ at time $t$
$x_i^t$: the position of particle $i$ at time $t$
$p$ = local best so far
$g$ = global best so far
$c_1,c_2$ = cognitive or social coefficients to pull the update to personal best or global best, ranging from 0 - 1
$r_1, r_2$ = randomization weights for velocity updates, ranging from 0 - 1
Firefly algorithm
 Assumptions
Assumptions
- The intensity of flashing lights is the sole factor that causes fireflies to be attracted to each other. The brightness is determined by the value of the objective function at it’s current position.
- The brighter the light, the more attractive (hahaaa if it was only this simple). If there is no light, then the firefly will perform a random walk in the search space.
- The attractiveness between two fireflies is inversely proportional to the distance between them. The farther apart they are, the less they attract each other.
Brightness
Let $I_i$ be the brightness of firefly $i$, which is proportional to the objective function value $f(x_i)$.
The attractiveness $\beta$ between firefly $i$ and firefly $j$ is modelled by the exponential decay function $\beta(r_{ij}) = \beta_0 \cdot e^{-\gamma \cdot r_{ij}^2}$. This should make sense if a firefly descends into another in circles.
Where:
$\beta_0$: The maximum attractiveness experienced when the distance is 0 (this being a constant is really funny, interpretively)
$\gamma$: A light absorption coefficient that determines the decay rate of the attraction.
$r_{ij}$: the Euclidean distance between firefly $i$ and firefly $j$ i.e. $r_{ij} = ||(x_i-x_j)||$.
Movement
Basically we can take the PSO update rule and replace the ‘updating part’ with attractiveness and randomization terms.
$x_i^{t+1} = x_i^t + \beta(r_{ij}) \cdot (x_j^t - x_i^t) + \alpha \cdot \epsilon_i^t$
Where:
$\beta(r_{ij}) \cdot (x_j^t - x_i^t)$ is the attractiveness term pulling firefly $i$ towards $j$
$\alpha \cdot \epsilon_i^t$ is the randomization term, which is a random vector drawn from Gaussian distribution.
Flower pollination algorithm.
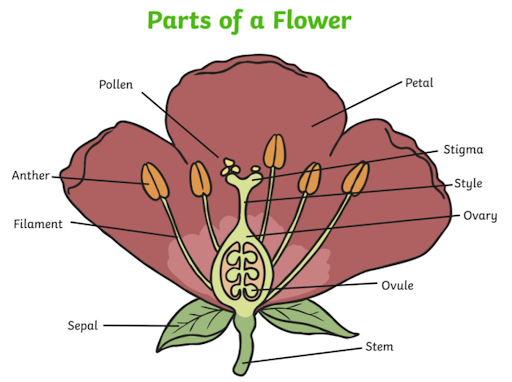 Forms of pollination:
Forms of pollination:
- Cross-Pollination: Pollen is transferred from one flower to another, often by pollinators like bees or birds from the anther to the surface of the stigma. This represents global exploration in the algorithm, where solutions (pollen) are shared between many distant flowers (solutions).
- Self-Pollination: Well, pollen is transferred within the same flower. This represents local exploitation in the algorithm, where solutions are refined locally. Only 10% of plants use this.
Pollen/flowers, what are they doing:
In the algorithm, one pollen grain represents a solution vector in the search space. The fitness of a solution is analogous to the reproductive success of the pollen’s derivative–a flower.
And pollinators too?
They act as vehicles for the pollen. Actually, pollinator flying distances aren’t Gaussian. Smaller steps are more common than longer ones in many fruit flies and animals. So we draw from a probability distribution that is heavy-tailed–Levy distribution.
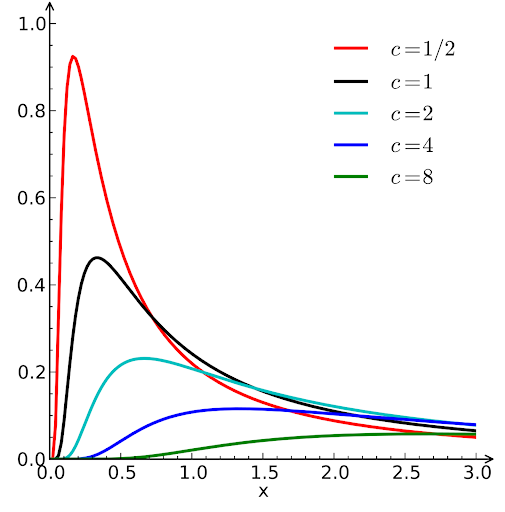
You can visualize it in 2D to get a better intuition.
 The area under the curve sums to one. So, we model distances using Levy flights to mimic the behavior of pollinators traveling between
flowers.
The area under the curve sums to one. So, we model distances using Levy flights to mimic the behavior of pollinators traveling between
flowers.
I should clarify the initialization will create a population of flowers, rather than pollinators/pollen with random positions $x_i$ respectively.
The main loop of the algorithm is still, like PSO, with a pollinator quirk in the updating part.
For each flower $i$, ‘flip a coin’ with value r between 0 and 1.
If r < p, perform global/cross pollination.
$x_i^{t+1} = x_i^t+ L \cdot (g - x_i^t)$
where $g$ is the current global best solution and $L$ is the key difference–a step size from a Levy distribution.
Otherwise, perform self-pollination.
$x_i^{t+1} = x_i^t + u \cdot (x_j^t - x_i^t)$
where $x_j^t$ and $x_k^t$ are two randomly selected flowers, and u is a step size from a uniform distribution.
The parasitic cuckoo
At this point you get the core idea of the swarm intelligence algorithms with their quirks in the updating rules so I will not belabour it further.
Here’s the story behind the cuckoo search algorithm. Parasitic cuckoos often choose a nest where the host bird laid their fresh eggs. Cuckoo hatchlings can kick eggs out of the nest! Some cuckoo species have evolved in such a way that female parasitic cuckoos are often very specialized in the mimicry of colour and pattern of the eggs of a few chosen host species.

Egg mimicry is not a conscious process but rather genetically determined. Likewise, a cuckoo chick can mimic the call of host chicks to gain access to more feeding opportunities.
So in the algorithm, we roughly have the following:
- The basic unit is the egg. Each egg represents a solution, the new egg laid by the cuckoo represents a new solution.
- Each cuckoo lays one egg at a randomly selected nest.
- Best nests with highest quality eggs are carried over to the next generation (of cuckoo eggs). the cuckoo egg will be selected when it’s the most similar to the high-quality eggs are solutions near-optimal value. the new solution will replace the worse solution. For simplicity, you may assume each nest only has a single egg which can be replaced. Though this may be generalized to having multiple eggs
- Host could discover a cuckoo egg with a probability. If the cuckoo egg fitness is less than the host bird, the egg is tossed out. Following, cuckoo may create a new one with simple random probability.
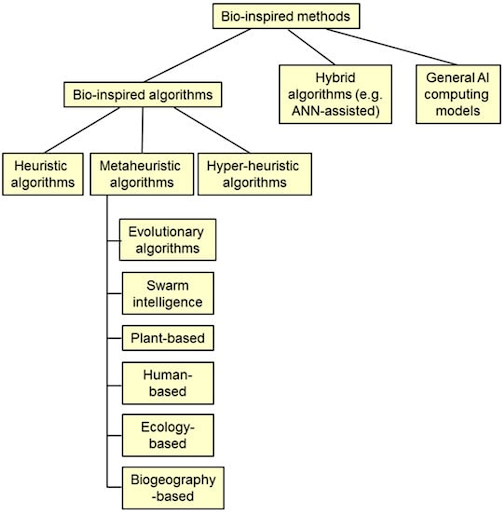
Taxonomies
There are a few hundreds of algorithms and an easy way to publish a paper is to laundry-list them and then benchmark on standard test functions. Which bio-inspired algorithms should we pay attention to?
| Zone of theory development e.g. Gray wolf algorithm |
Zone of application e.g. Bacterial foraging, firefly algorithm, cuckoo search, flower pollination |
| Zone of re-discovery e.g. leaping frog algorithm |
Zone of commercialization e.g. Ant colony optimization, genetic algorithm, particle swarm and neural networks |
Otherwise, the bio-inspired algorithms have been explored for various telecommunication applications, including routing in sensor networks, electromagnetic antenna design, mobility management, filter design, home automation networks, spectrum sensing in cognitive radio and Internet of Things as well as robotic bees!
“We mentioned swarm intelligence and bio-inspired algorithms. What is the relation between them? Swarm is a subset of bio-inspired algorithms, and descriptively, they’re becoming more meta over time.
Some demos
I made a 3D simulation in Unity during 2 weeks at Founders Inc AI x hardware residency with team Colony. My first time writing in C#. We also had a microdrone < 250g (material list)

Further reading/thoughts
- A salient application of swarm intelligence is UAVs for agtech or SLAM purposes (#startupideas). I’d be very curious to see your prototypes or consider collaborating!
- Bio-mimicry Institute Go ahead and get inspired by all sorts of natural strategies!
- Robotic bees. The vision is to apply swarm intelligence to embodied swarm of bees! I’d be curious to know what the progress update is with the wyss institute. Last time I checked (2019), they flew untethered for less than a min. If you’re strong at hardware and looking for a mission to devote yourself to for at least several months, check it out.
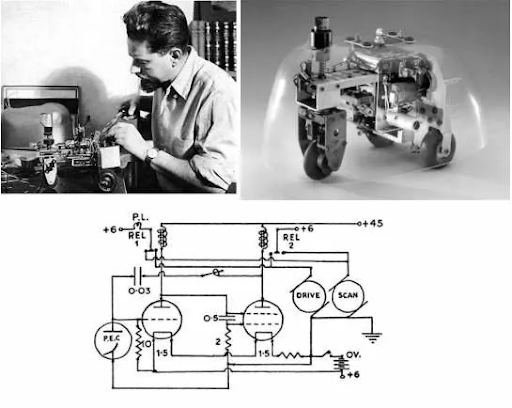
- Another direction you can go in is cybernetics. In the late 1940s, Grey Walter sought was building turtoise robots to showcase emergence from simple non-linear dynamics. So it could move toward light (phototaxis), avoid obstacles and charge itself when power is low. It’s groundbreaking at the time and fundamental in today’s robotics. It seems like robotics is heavily bio-inspired in general but we don’t see this frame.